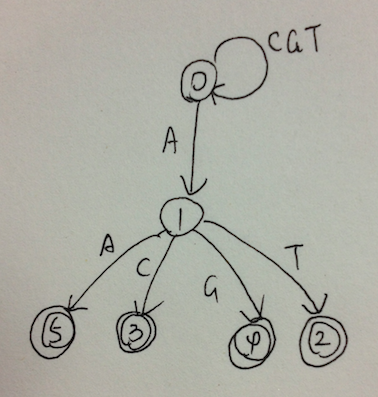
trie图
题意是,输入m个禁忌字符串,和长度n,问只包含’A’、’C’、’G’和’T’4种字符的总长为n且不包含任一禁忌字符串的字符串总数是多少。
利用trie图建立的DFA,可以根据安全状态间的状态转移来得到总长为k的安全字符串总数。
例如,对于sample数据:
|
1 2 3 4 5 |
4 3 AT AC AG AA |
其中安全结点为根结点0和接收到’A’之后的结点1。他们之间的状态转移为0->0(3重)、0->1,用矩阵表示就是:
|
1 2 3 4 5 6 |
3 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
用该矩阵与向量(1,1,1,1,1,1)相乘k次,即可得到从各个点出发长度为k的安全字符串总数。而题目本身n最多是2*10^9的,刚好适合用矩阵幂乘来O(l^2*log(n))地得到结果,这里l是结点总数,最多10个长度为10的禁忌字符串,因此DFA图中最多包含101个结点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 |
#include<queue> #include<cstdio> #include<cstring> using namespace std; #define ll long long int m,n,el,root,si[128]; char s[11]; ll a[101][101],b[101][101],c[101][101]; struct E { int b,c,fa,sp,p[4]; }e[101]; void init() { int i,j,k,l; el=0; memset(e,0,sizeof e); root=el++; while(m--) { scanf("%s",s); for(i=0,l=root;s[i];i++) { if(!e[l].p[si[s[i]]]) { e[l].p[si[s[i]]]=el++; e[e[l].p[si[s[i]]]].fa=l; e[e[l].p[si[s[i]]]].c=si[s[i]]; } l=e[l].p[si[s[i]]]; } e[l].b=1; } queue<int>Q; Q.push(root); while(!Q.empty()) { i=Q.front(); Q.pop(); if(e[i].fa!=root) e[i].sp=e[e[e[i].fa].sp].p[e[i].c]; e[i].b|=e[e[i].sp].b; e[i].b|=e[e[i].fa].b; for(l=0;l<4;l++) { if(e[i].p[l]) Q.push(e[i].p[l]); else e[i].p[l]=e[e[i].sp].p[l]; } } } void mul(ll a[101][101],ll b[101][101]) { int i,j,k,l; for(i=0;i<el;i++) for(j=0;j<el;j++) { c[i][j]=0; for(k=0;k<el;k++) c[i][j]+=a[i][k]*b[k][j]; c[i][j]%=100000; } memcpy(a,c,sizeof c); } void solve() { int i,j,k,l; memset(a,0,sizeof a); memset(b,0,sizeof b); for(i=0;i<el;i++) if(!e[i].b) for(l=0;l<4;l++) if(!e[e[i].p[l]].b) a[i][e[i].p[l]]++; for(i=0;i<el;i++) b[i][i]=1; while(n) { if(n&1) mul(b,a); n>>=1; mul(a,a); } for(i=j=0;i<el;i++) j=(j+b[0][i])%100000; printf("%d\n",j); } int main() { si['A']=0; si['C']=1; si['G']=2; si['T']=3; while(~scanf("%d%d",&m,&n)) { init(); solve(); } return 0; } |
另外,这题应该是根据Censored!修改来的。后者与本题的区别仅在于字符数更多,不需要矩阵幂乘,但要用到高精度(其实还有OTL的unicode字符输入,阴了好多人)……