The Bermuda Triangle

搜索

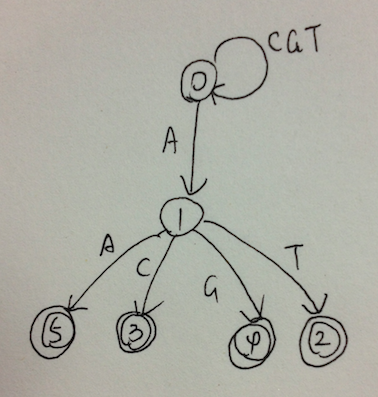
题意：给出一个边长以三角形个数描述的正六边形，以及n种正三角形，问该六边形能否刚好由这些三角形完全覆盖。

放假都没做题，有点手生。由于提示是搜索题，首先考虑问题建模。可以将每个小三角形的覆盖情况用1bit表示，那么六边形的每行就可以用一个位向量来描述。用作覆盖的三角形只会是正置或倒置。于是，问题就转化成了由上到下由左到右地依次尝试用各种三角形进行填充。

需要注意的是，正六边形是对称的，可以分解成6个正三角形或3个菱形，直接判断后者的完全覆盖情况即可。对于此题数据，只分解成正三角形会WA，分解成菱形可以AC。另外，如果是原来的正六边形，一行最多会有25*4-1=99个小三角形，就无法用64位的LL来表示了。而菱形的话，一行最多为25*2=50位，还是可以的，写起来也较易实现。

ps: 这个假期过得太开心了……发生了不少好事情，希望不会是把一年的运气都一下子用光了吧…………那么接下来，就是要好好准备3月中旬的校赛了。

Sequence Partitioning

单调队列 + 二分 + DP

题意：输入为n对数字(ai,bi)，以及m，需要将这n对数字按原始顺序划分为p组，需要满足：（1）前一组的各bi都比后一组的各ai大；（2）各组中最大的ai的和小于等于m。在该条件下进行的划分，将各组bi求和，取其中的最大值。求解目标是最小化该最大值。

非常拗口的题意……但仔细分析之后可以发现条件（1）中规定了n对数之间的哪些位置可以进行划分，而且这些划分位置之间是相互独立的，也即某个位置实际进行划分之后，不影响其他位置的可划分性。这里可以利用单调队列，边遍历数组边记录a的剩余最大值和b的累计最小值来记录各个可划分的位置，处理的时间是O(n)的。

随后分析求解目标，可以得到最大值的存在性是单调的，因此可以二分最大分组b值和，每次判断是否能满足条件（2）。

对条件（2）的判断，可以用DP来实现，对于每个可行的划分位置，计算满足二分值的划分范围内最大a值的累计最小值。这里同样可以利用单调队列作优化。

但即使这样，极端情况下时间复杂度其实是要O(n^2*lgk)的。能过题目，大概也是数据不够强。

相关类型的题目，推荐这篇文章，总结得很好。

<也啰嗦一点自己的想法>
最近几天研究的单调队列确实是非常独特的数据结构，稍作小结的话，可以发现常用的维护区间信息的数据结构好多，包括：线段树，树状数组，用于离线rmq的st算法，以及现在学到的单调队列。如果要进行比较的话，大致如下：

线段树：应该算是最灵活的数据结构。更新、查询信息可以针对点，也可以针对区间，每次操作时间复杂度是O(lgn)。但实现起来细节较多。

树状数组：轻便的数据结构，易于扩展到多维。更新只能针对点，查询的是区间，每次操作都是O(lgn)。相对于线段树，缺点是灵活性较差，难以应用于不同类型的题目。

st算法：不同于以上两个在线算法，st是离线的。首先O(nlgn)地构造一个保存预处理信息的数组，以后每次查询信息的时间复杂度都是O(1)的。该算法几乎算是“模块化”的，因此很易与其他算法结合使用。典型应用是后缀数组。

单调队列：需要在遍历数组的同时，动态地维护当前有效区间内的信息。仅适用于已知区间长度限制的情况，但时间复杂度非常优秀，达到O(n)。

如果可以一直这样做题下去的话…………还能学到多少呢？
<⁄啰嗦完毕>

最后，快放假了，也预祝各位新年愉快。

DNA Sequence

trie图

题意是，输入m个禁忌字符串，和长度n，问只包含’A’、’C’、’G’和’T’4种字符的总长为n且不包含任一禁忌字符串的字符串总数是多少。

利用trie图建立的DFA，可以根据安全状态间的状态转移来得到总长为k的安全字符串总数。

例如，对于sample数据：

建好的trie图为：

其中安全结点为根结点0和接收到’A’之后的结点1。他们之间的状态转移为0->0(3重）、0->1，用矩阵表示就是：

用该矩阵与向量(1,1,1,1,1,1)相乘k次，即可得到从各个点出发长度为k的安全字符串总数。而题目本身n最多是2*10^9的，刚好适合用矩阵幂乘来O(l^2*log(n))地得到结果，这里l是结点总数，最多10个长度为10的禁忌字符串，因此DFA图中最多包含101个结点。

另外，这题应该是根据Censored!修改来的。后者与本题的区别仅在于字符数更多，不需要矩阵幂乘，但要用到高精度（其实还有OTL的unicode字符输入，阴了好多人）……

Word Puzzles

trie图

题意：输入一个r*c的字符矩阵，以及w个单词，每个单词会在字符矩阵中以某种方式出现一次。这里“某种方式”是指单词起始位置任意，其余部分沿横竖斜共8个方向中的一种直列排布。要求的就是各个单词以“哪种方式”出现。

如果是单模式匹配，可以采用滚动hash、trie树、kmp等等。但这里是多模式匹配，因此需要用到trie图，也即有穷自动机（DFA）。建图的方式参考了王赟的《Trie 图的构建、活用与改进》。基本做法是，根据w个单词建好trie树后，补全树上尚未定义的状态转移即可得到trie图。其中关键思想在于，若从某结点出发的目标字符对应状态在树中不存在，则指向其后缀结点的目标字符子结点。这里某结点的后缀结点指的是，该结点对应字符串去掉头字符后在trie树上的匹配终结点，具体可以根据该结点的父结点的后缀结点计算得到。可以发现，某结点的深度必定是大于其后缀结点的，因此，可以通过BFS的方式依次补齐trie树上各层结点的状态转移来得到trie图。而对于匹配是否成功，存在一个定理：某结点能匹配成功当且仅当其后缀结点能匹配成功。

回到题目，由于题目本身已经明确每个单词刚好仅在原字符矩阵出现一次。因此枚举8个方向，依次从各起始结点在trie图上作状态转移，每当遇到终结点时记录对应字符串的匹配信息即可。

内存开小了RE了一次，然后AC的程序也很慢……不过总体来说还算是挺顺利的。

ps：唠叨点题外话，很多字符串算法貌似都只对英语有效呢，使用大数组来余存储匹配信息的做法对于中文或其他多字符语言却不太适用。其他的领域，包括分词、语法分析等等，貌似也是英语比较容易处理。会有那么一天，由于技术极致发展催生出的工业需求，反过来局限人类文明的进步吗？

Command Network

有向图最小生成树

需要用到朱刘-Edmonds算法。算法的基本步骤很简单（证明就略过了）：
（1）从源点出发DFS，若无法到达所有点，最小生成树不存在，直接返回；
（2）找每个结点的最小权入边；
（3）若存在环，将同一环上所有结点进行缩点，对于指向该环内某点的边，将其权值减去该点的最小入边权，重复（2）；若无环，则树已建成。

但实现这个算法却想了整整一天。

分析算法步骤可以发现，（2）中每次选中的各个最小权，其值都属于最小生成树的一部分，一旦某边被选中后，其权值将确定不再修改。因此可以考虑对边作一个标记，表示是否已选走，之后找环时可以直接忽略这些边。另外，缩点操作可能使某些边变成自环，这些边也是要忽略的。

（3）找环时，可以考虑标记各个点，每次从无标记的某个点出发沿入边回溯，若遇到标记相同的点表示找到了环，此时可继续回溯将环上所有点标记为第t步找出的环。然后就是缩点，这里我用到了并查集。首先，需要修改各入边权值。然后，记录各个环上的点原本的父结点，再依次将环上各点与其父结点作并集。最后，将生成的新点入边权值更新为无穷大。这里需要记录原父结点是因为并查集缩点后原来的结点编号就失效了，因此环信息也就被破坏了（在这一步DEBUG了很久才发现问题……）。

最后就是遍历整个边表，将各个有标记的边权值相加，即为最小生成树权值。

时间复杂度方面，迭代部分的找最小权入边O(E)，找环O(V)，更新边权值O(E)，缩点O(V)。以上这些操作最多迭代O(V)次，因此总体时间复杂度是O(VE)的。实在是很漂亮的算法……

ps：做题到现在为止，第一次用到中国人发明的算法。两位作者中，我只搜到了朱永津，只有这篇文章讲得稍微多点，相关资料出奇的少呢……

Jamie’s Contact Groups

二分 + 最大流

输入为n、m，分别表示有n个点，每个点可以属于m种分类里面的某几种，将n个点分类（使每个点仅属于某一类）后，设最大的类里含有g个点，目标就是最小化g。

模型很简单，源点到n个点有容量为1的边，n个点到各自的分类有边，m个分类到汇点各有容量为g的边。然后就是二分g的值，每次用网络流判断是否可行。

但是……到这里明明就很清晰的思路，就是给我无限TLE……在明确其他部分都没得改进后，发现是网络流算法本身太慢……一直以来都只会用EK，而可能由于做过的题目都太水了……竟然都没有被卡过TLE。这次总算栽跟头了。于是，根据这篇文章学了一下ISAP，然后用自己的数据结构来实现也很简单，一下下就AC了：