分类目录归档：acm

[POJ 3169]

差分约束系统。

有n只牛，每只牛i对应x轴上一点di，对于i < j，有di <= dj。存在ml个关系di >= dj – k，其中i < j；又存在md个关系di <= dj - k，其中i < j。要求d[n] - d[1]最大值。若关系无法满足，输出-1；若最大值为无穷，输出-2。由于题目所求的是限制约束下的最大值，也即需要取大于等于号建立差分约束系统，那么3种边分别有： dj >= di
di + k >= dj
dj – k >= di

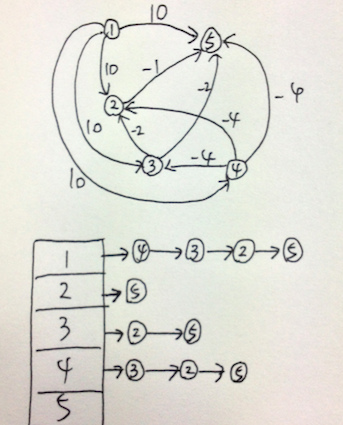
初始化除d1外的di值为无穷大，便可以用SPFA求解了。每次当 di + k < dj 时，进行松弛 dj = di + k。但是……用栈跑SPFA时却无限WA。换成队列一下就AC了。找到了原始数据后又看了别人的程序，最后发现问题出在了判负环上。基于队列的SPFA是用入栈次数>n来判断是否存在负环的，而姜碧野的《SPFA算法的优化与应用》中深搜的SPFA通过节点是否在栈中判负环是针对递归实现的。而我写的是基于栈的非递归SPFA，用的还是根据入栈次数>n判负环，但却发现很易出现误判。猜测由于深搜SPFA可以说是“盲目”推进的，也即有可能过多地沿回边更新，而导致入栈次数超过n，但实际却不存在负环。例如下图的例子：

最后的解是d[1..5] = {0, 4, 6, 10, 3}，其中结点5的入栈次数高达8次，但仍是无负环的。

在这题中，如果改变邻接表中边的顺序，让深搜SPFA尽量往图的深处推进，就能使用入栈次数来正确地判断负环了。可惜没有找到通用的严格证明……

#include<cstdio>
#include<cstring>

int n,ml,md,hd[1001],el,d[1001],b[1001],c[1001];
int stk[1000],sl;

struct E
{
    int v,d,p;
}e[100000];

inline void adde(int u,int v,int d)
{
    e[el].v=v; e[el].d=d; e[el].p=hd[u]; hd[u]=el++;
}

void init()
{
    int i,j,k,l;
    el=0;
    sl=0;
    memset(hd,-1,sizeof hd);
    memset(b,0,sizeof b);
    memset(c,0,sizeof c);
    for(i=1;i<=n;i++)
        d[i]=0x7fffffff;
    while(ml--)
    {
        scanf("%d%d%d",&i,&j,&k);
        adde(i,j,k);
    }
    while(md--)
    {
        scanf("%d%d%d",&i,&j,&k);
        adde(j,i,-k);
    }
    for(i=2;i<=n;i++)
        adde(i,i-1,0);
}

int solve()
{
    int i,j,k,l;
    b[1]=1;
    d[1]=0;
    stk[sl++]=1;
    while(sl)
    {
        i=stk[--sl];
        b[i]=0;
        for(l=hd[i];l!=-1;l=e[l].p)
        {
            j=e[l].v;
            k=e[l].d;
            if(d[i]+k<d[j])
            {
                d[j]=d[i]+k;
                if(!b[j])
                {
                    if(++c[j]>n)
                        return -1;
                    b[j]=1;
                    stk[sl++]=j;
                }
            }
        }
    }
    if(d[n]==0x7fffffff)
        return -2;
    return d[n]-d[1];
}

int main()
{
    int i,j;
    while(~scanf("%d%d%d",&n,&ml,&md))
    {
        init();
        printf("%d\n",solve());
    }
    return 0;
}

#include<cstdio>

#include<cstring>

int n,ml,md,hd[1001],el,d[1001],b[1001],c[1001];

int stk[1000],sl;

struct E

{

int v,d,p;

}e[100000];

inline void adde(int u,int v,int d)

{

e[el].v=v; e[el].d=d; e[el].p=hd[u]; hd[u]=el++;

}

void init()

{

int i,j,k,l;

el=0;

sl=0;

memset(hd,-1,sizeof hd);

memset(b,0,sizeof b);

memset(c,0,sizeof c);

for(i=1;i<=n;i++)

d[i]=0x7fffffff;

while(ml--)

{

scanf("%d%d%d",&i,&j,&k);

adde(i,j,k);

}

while(md--)

{

scanf("%d%d%d",&i,&j,&k);

adde(j,i,-k);

}

for(i=2;i<=n;i++)

adde(i,i-1,0);

}

int solve()

{

int i,j,k,l;

b[1]=1;

d[1]=0;

stk[sl++]=1;

while(sl)

{

i=stk[--sl];

b[i]=0;

for(l=hd[i];l!=-1;l=e[l].p)

{

j=e[l].v;

k=e[l].d;

if(d[i]+k<d[j])

{

d[j]=d[i]+k;

if(!b[j])

{

if(++c[j]>n)

return -1;

b[j]=1;

stk[sl++]=j;

}

if(d[n]==0x7fffffff)

return -2;

return d[n]-d[1];

}

int main()

{

int i,j;

while(~scanf("%d%d%d",&n,&ml,&md))

{

init();

printf("%d\n",solve());

}

return 0;

}

结论就是：下次还是老老实实用队列判负环吧……

[POJ 2165]

发表回复

Gunman

计算几何。

题意是，在一个三维直角坐标系上，有平行于xOy平面的n个矩形，其边与x、y轴平行，坐标取值范围(0,1000)。问在x轴上是否存在一点能引出一条直线与所有矩形都相交。

这题读完后，并没有太直观的思路。但由于数据规模不大，考虑用三分法。每次对枚举的double m，按z值的增序遍历所有矩形，维护一个窗口作为能与所有矩形都相交的区域，最后返回相交矩形的数目。基本的想法是，由于矩形是连续且规则的图形，那么若解存在，则必定有最大值为n的单峰存在。但WA了数次后发现，由于返回值是离散的，就无法通过严格单调性来对三分法上下界进行修改了。

随后又发现，m值的所有可能取值其实是有限的，为某两个矩形i和j间(xi,0,zi)与(xj,0,zj)所确定的直线与x轴的交点，这里xi或xj可以是矩形的左或右边界。因此枚举的m值总数是O(n^2)的。而用前面描述的遍历方法便能确定从该点出发是否与所有矩形相交。所以总复杂度是O(n^3)的。在n=100的情况下，是可以AC的。最后跑了235ms。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

#define eps 1e-8

int n;
double x1[100],y1[100],x2[100],y2[100],z[100];

void init()
{
    int i;
    for(i=0;i<n;i++)
        scanf("%lf%lf%lf%lf%lf",x1+i,y1+i,x2+i,y2+i,z+i);
}

int calc(double m)
{
    int i,d;
    double xl,yb,xr,yt;
    for(xl=x1[0],yb=y1[0],xr=x2[0],yt=y2[0],i=1,d=1;i<n;i++)
    {
        xl=m+(xl-m)/z[i-1]*z[i]; yb=yb/z[i-1]*z[i];
        xr=m+(xr-m)/z[i-1]*z[i]; yt=yt/z[i-1]*z[i];
        xl=min(xr,max(xl,x1[i]));
        yb=min(yt,max(yb,y1[i]));
        xr=max(xl,min(xr,x2[i]));
        yt=max(yb,min(yt,y2[i]));
        if(xl>x1[i]-eps&&xl<x2[i]+eps
                &&yb>y1[i]-eps&&yb<y2[i]+eps)
            d++;
    }
    return d;
}

void mksol(double m)
{
    int i;
    double xl,yb,xr,yt;
    puts("SOLUTION");
    printf("%.6f\n",m);
    for(xl=x1[0],yb=y1[0],xr=x2[0],yt=y2[0],i=1;i<n;i++)
    {
        xl=m+(xl-m)/z[i-1]*z[i]; yb=yb/z[i-1]*z[i];
        xr=m+(xr-m)/z[i-1]*z[i]; yt=yt/z[i-1]*z[i];
        xl=min(xr,max(xl,x1[i]));
        yb=min(yt,max(yb,y1[i]));
        xr=max(xl,min(xr,x2[i]));
        yt=max(yb,min(yt,y2[i]));
    }
    for(i=0;i<n;i++)
        printf("%.6f %.6f %.6f\n",m+(xl-m)/z[n-1]*z[i],
                yb/z[n-1]*z[i],z[i]);
}

void solve()
{
    int i,j;
    double m;
    for(i=0;i<n-1;i++)
    {
        for(j=i+1;j<n;j++)
        {
            m=x1[i]-z[i]*(x1[i]-x2[j])/(z[i]-z[j]);
            if(calc(m)==n)
                break;
            m=x1[i]-z[i]*(x1[i]-x1[j])/(z[i]-z[j]);
            if(calc(m)==n)
                break;
            m=x2[i]-z[i]*(x2[i]-x1[j])/(z[i]-z[j]);
            if(calc(m)==n)
                break;
            m=x2[i]-z[i]*(x2[i]-x2[j])/(z[i]-z[j]);
            if(calc(m)==n)
                break;
        }
        if(j<n)
            break;
    }
    if(i==n-1)
        puts("UNSOLVABLE");
    else
        mksol(m);
}

int main()
{
    while(~scanf("%d",&n))
    {
        init();
        solve();
    }
    return 0;
}

#include<cstdio>

#include<cstring>

#include<algorithm>

using namespace std;

#define eps 1e-8

int n;

double x1[100],y1[100],x2[100],y2[100],z[100];

void init()

{

int i;

for(i=0;i<n;i++)

scanf("%lf%lf%lf%lf%lf",x1+i,y1+i,x2+i,y2+i,z+i);

}

int calc(double m)

{

int i,d;

double xl,yb,xr,yt;

for(xl=x1[0],yb=y1[0],xr=x2[0],yt=y2[0],i=1,d=1;i<n;i++)

{

xl=m+(xl-m)/z[i-1]*z[i]; yb=yb/z[i-1]*z[i];

xr=m+(xr-m)/z[i-1]*z[i]; yt=yt/z[i-1]*z[i];

xl=min(xr,max(xl,x1[i]));

yb=min(yt,max(yb,y1[i]));

xr=max(xl,min(xr,x2[i]));

yt=max(yb,min(yt,y2[i]));

if(xl>x1[i]-eps&&xl<x2[i]+eps

&&yb>y1[i]-eps&&yb<y2[i]+eps)

d++;

}

return d;

}

void mksol(double m)

{

int i;

double xl,yb,xr,yt;

puts("SOLUTION");

printf("%.6f\n",m);

for(xl=x1[0],yb=y1[0],xr=x2[0],yt=y2[0],i=1;i<n;i++)

{

xl=m+(xl-m)/z[i-1]*z[i]; yb=yb/z[i-1]*z[i];

xr=m+(xr-m)/z[i-1]*z[i]; yt=yt/z[i-1]*z[i];

xl=min(xr,max(xl,x1[i]));

yb=min(yt,max(yb,y1[i]));

xr=max(xl,min(xr,x2[i]));

yt=max(yb,min(yt,y2[i]));

}

for(i=0;i<n;i++)

printf("%.6f %.6f %.6f\n",m+(xl-m)/z[n-1]*z[i],

yb/z[n-1]*z[i],z[i]);

}

void solve()

{

int i,j;

double m;

for(i=0;i<n-1;i++)

{

for(j=i+1;j<n;j++)

{

m=x1[i]-z[i]*(x1[i]-x2[j])/(z[i]-z[j]);

if(calc(m)==n)

break;

m=x1[i]-z[i]*(x1[i]-x1[j])/(z[i]-z[j]);

if(calc(m)==n)

break;

m=x2[i]-z[i]*(x2[i]-x1[j])/(z[i]-z[j]);

if(calc(m)==n)

break;

m=x2[i]-z[i]*(x2[i]-x2[j])/(z[i]-z[j]);

if(calc(m)==n)

break;

}

if(j<n)

break;

}

if(i==n-1)

puts("UNSOLVABLE");

else

mksol(m);

}

int main()

{

while(~scanf("%d",&n))

{

init();

solve();

}

return 0;

}

[POJ 2043]

发表回复

Area of Polygons

计算几何。

题意是，给出一个多边形的顶点（坐标都为整数）描述，要求该多边形在网格上覆盖的格子数目。

基本思路是扫描线，从左到右，同时维护一个有序数组s，记录当前区间内存在的线段的y值，线段必定是成对出现的，且每对线段间的区域为多边形内部。这样就可以计算每个区间内被覆盖的格子数了。

具体的实现上，首先初始化所有的n条线段，并放入一个表头大小为4001的邻接表中，方便扫描线时将新扫到的线段加入。垂直的线段直接忽略。对线段结构体记录其当前y值，斜率k，终点xr，以及删除标记b。每次处理一个区间的线段时，删除线段即为将标记位置1。对s内的线段排序时，首先将被删除的线段都放到最后，然后若y值不同则按y从小到大排序，否则再按斜率k从小到大排序。

计算每段区间[x,x+1]内被覆盖的格子数时，需要注意若连续的多条线段过于接近，要避免重复计算。同时取floor或ceil时，需要对y值增或减eps，以舍去计算误差。

总体上来说虽然细节较多，仔细思考后还是比较顺利地1A了。不过也写了一整个下午……

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;

#define eps 1e-8

int n,hd[4001],el,ans,sl;
int x[100],y[100],mnx,mxx;

struct E
{
    double y,k;
    int b,xr,p;
}e[100],s[100];

struct CP
{
    bool operator () (const E &p,const E &q) const
    {
        if(p.b>q.b) return 0;
        if(p.b<q.b) return 1;
        if(abs(p.y-q.y)>eps)
            return p.y<q.y;
        else
            return p.k<q.k;
    }
};

inline void adde(int x0,int y0,int x1,int y1)
{
    if(x0==x1) return;
    if(x0>x1)
    {
        x0^=x1^=x0^=x1;
        y0^=y1^=y0^=y1;
    }
    e[el].y=y0;
    e[el].k=1.0*(y1-y0)/(x1-x0);
    e[el].b=0;
    e[el].xr=x1;
    e[el].p=hd[x0];
    hd[x0]=el++;
}

void init()
{
    int i,j,k,l;
    el=sl=ans=0;
    mnx=4001;
    mxx=0;
    memset(hd,-1,sizeof hd);
    for(i=0;i<n;i++)
    {
        scanf("%d%d",&x[i],&y[i]);
        x[i]+=2000;
        y[i]+=2000;
        mxx=max(mxx,x[i]);
        mnx=min(mnx,x[i]);
    }
    adde(x[n-1],y[n-1],x[0],y[0]);
    for(i=0;i<n-1;i++)
        adde(x[i],y[i],x[i+1],y[i+1]);
}

void solve()
{
    int i,j,k,l;
    double yb,yt;
    E *p,*q;
    for(i=mnx;i<mxx;i++)
    {
        k=ans;
        for(l=0;l<sl&&!s[l].b;l++)
        {
            if(s[l].xr==i)
                s[l].b=1;
        }
        for(l=hd[i];l!=-1;l=e[l].p)
            s[sl++]=e[l];
        sort(s,s+sl,CP());
        if(s[0].b)
            continue;
        yt=-1e30;
        for(l=0;l<sl&&!s[l].b;l+=2)
        {
            p=&s[l];
            q=&s[l+1];
            yb=min(floor(p->y+eps),floor(p->y+p->k+eps));
            if(yb<yt)
                yb=yt;
            yt=max(ceil(q->y-eps),ceil(q->y+q->k-eps));
            p->y+=p->k;
            q->y+=q->k;
            ans+=yt-yb;
        }
    }
    printf("%d\n",ans);
}

int main()
{
    while(~scanf("%d",&n)&&n)
    {
        init();
        solve();
    }
    return 0;
}

100

101

102

103

104

105

106

107

108

109

110

#include<cstdio>

#include<cstring>

#include<cmath>

#include<algorithm>

using namespace std;

#define eps 1e-8

int n,hd[4001],el,ans,sl;

int x[100],y[100],mnx,mxx;

struct E

{

double y,k;

int b,xr,p;

}e[100],s[100];

struct CP

{

bool operator () (const E &p,const E &q) const

{

if(p.b>q.b) return 0;

if(p.b<q.b) return 1;

if(abs(p.y-q.y)>eps)

return p.y<q.y;

else

return p.k<q.k;

}

};

inline void adde(int x0,int y0,int x1,int y1)

{

if(x0==x1) return;

if(x0>x1)

{

x0^=x1^=x0^=x1;

y0^=y1^=y0^=y1;

}

e[el].y=y0;

e[el].k=1.0*(y1-y0)/(x1-x0);

e[el].b=0;

e[el].xr=x1;

e[el].p=hd[x0];

hd[x0]=el++;

}

void init()

{

int i,j,k,l;

el=sl=ans=0;

mnx=4001;

mxx=0;

memset(hd,-1,sizeof hd);

for(i=0;i<n;i++)

{

scanf("%d%d",&x[i],&y[i]);

x[i]+=2000;

y[i]+=2000;

mxx=max(mxx,x[i]);

mnx=min(mnx,x[i]);

}

adde(x[n-1],y[n-1],x[0],y[0]);

for(i=0;i<n-1;i++)

adde(x[i],y[i],x[i+1],y[i+1]);

}

void solve()

{

int i,j,k,l;

double yb,yt;

E *p,*q;

for(i=mnx;i<mxx;i++)

{

k=ans;

for(l=0;l<sl&&!s[l].b;l++)

{

if(s[l].xr==i)

s[l].b=1;

}

for(l=hd[i];l!=-1;l=e[l].p)

s[sl++]=e[l];

sort(s,s+sl,CP());

if(s[0].b)

continue;

yt=-1e30;

for(l=0;l<sl&&!s[l].b;l+=2)

{

p=&s[l];

q=&s[l+1];

yb=min(floor(p->y+eps),floor(p->y+p->k+eps));

if(yb<yt)

yb=yt;

yt=max(ceil(q->y-eps),ceil(q->y+q->k-eps));

p->y+=p->k;

q->y+=q->k;

ans+=yt-yb;

}

printf("%d\n",ans);

}

int main()

{

while(~scanf("%d",&n)&&n)

{

init();

solve();

}

return 0;

}

[POJ 3130]

发表回复

How I Mathematician Wonder What You Are!

判断多边形内核。

题意为N个顶点逆时针顺序描述的一个多边形，要求判断该多边形是否有“内核”。所谓“内核”，就是在该多边形内的一块区域，站在这块区域内任意一点观察多边形的内部，都可以无死角地看遍整个多边形。

解这题涉及到半平面的概念。其实就是每条线段都会将平面区域划分成两部分，一部分包含多边形内部，一部分不包含。那么，将所有线段对应的包含多边形内部那一半的平面区域求交集，就得到了多边形的内核（如果存在）或者空集（不存在内核）。

进一步考虑实现问题的话，可以将每条直线描述为ax+by+c=0，那么半平面方程即为ax+by+c>=0，其中a、b、c三个系数，根据直线的朝向以及题目给定的逆时针顺序，a是取-1或1的，进而可以确定b和c。多边形的内核区域，可以抽象为某些点，进一步分析可以发现，若存在内核，则其角一定是某两条边所在直线的交点。由于最多只有50条边，那么可以枚举n(n-1)/2个交点，依次代入n个半平面方程，看是否存在点满足对所有半平面方程都大于0即可。

#include<cstdio>
#include<cstring>
#include<list>
using namespace std;

#define eps 1e-8

int n,el,ll,hd;
double x[50],y[50];

struct L
{
    double a,b,c;
}l[50];

struct E
{
    double x,y;
    E(double a,double b): x(a),y(b) {};
};

list<E>L;

inline double abs(double a)
{
    return a>0?a:-a;
}

inline void addl(double x1,double y1,double x2,double y2)
{
    double xd,yd,a,b,c;
    if(abs(xd=x2-x1)<eps)
    {
        if(y2<y1)
        {
            a=1;
            c=-x1;
        }
        else
        {
            a=-1;
            c=x1;
        }
        b=0;
    }
    else if(abs(yd=y2-y1)<eps)
    {
        a=0;
        if(x2>x1)
        {
            b=1;
            c=-y1;
        }
        else
        {
            b=-1;
            c=y1;
        }
    }
    else
    {
        a=1;
        b=(x2-x1)/(y1-y2);
        c=-x1-b*y1;
        if(yd>0)
        {
            a=-a; b=-b; c=-c;
        }
    }
    l[ll].a=a; l[ll].b=b; l[ll].c=c; ll++;
}

inline void adde(int i,int j)
{
    double a1=l[i].a,b1=l[i].b,c1=l[i].c;
    double a2=l[j].a,b2=l[j].b,c2=l[j].c;
    if(abs(a1)<eps&&abs(a2)<eps||abs(b1)<eps&&abs(b2)<eps)
        return;
    if(abs(a1/b1-a2/b2)<eps)
        return;
    double x,y;
    if(abs(a1)<eps)
    {
        y=-c1/b1;
        x=-(b2*y+c2)/a2;
    }
    else if(abs(b1)<eps)
    {
        x=-c1/a1;
        y=-(c2+a2*x)/b2;
    }
    else
    {
        y=(a2/a1*c1-c2)/(b2-a2/a1*b1);
        x=-(b1*y+c1)/a1;
    }
    L.push_back(E(x,y));
}

void init()
{
    int i,j,k;
    L.clear();
    hd=-1;
    el=ll=0;
    for(i=0;i<n;i++)
        scanf("%lf%lf",&x[i],&y[i]);
    for(i=0;i<n-1;i++)
        addl(x[i],y[i],x[i+1],y[i+1]);
    addl(x[n-1],y[n-1],x[0],y[0]);
    for(i=0;i<n-1;i++)
        for(j=i+1;j<n;j++)
            adde(i,j);
}

void solve()
{
    int i,j,k;
    double a,b,c,x,y;
    list<E>::iterator lit;
    for(i=0;i<ll;i++)
    {
        a=l[i].a; b=l[i].b; c=l[i].c;
        for(lit=L.begin();lit!=L.end();)
        {
            x=lit->x; y=lit->y;
            if(a*x+b*y+c<-eps)
                L.erase(lit++);
            else
                lit++;
        }
    }
    if(L.size())
        puts("1");
    else
        puts("0");
}

int main()
{
    while(~scanf("%d",&n)&&n)
    {
        init();
        solve();
    }
    return 0;
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

#include<cstdio>

#include<cstring>

#include<list>

using namespace std;

#define eps 1e-8

int n,el,ll,hd;

double x[50],y[50];

struct L

{

double a,b,c;

}l[50];

struct E

{

double x,y;

E(double a,double b): x(a),y(b) {};

};

list<E>L;

inline double abs(double a)

{

return a>0?a:-a;

}

inline void addl(double x1,double y1,double x2,double y2)

{

double xd,yd,a,b,c;

if(abs(xd=x2-x1)<eps)

{

if(y2<y1)

{

a=1;

c=-x1;

}

else

{

a=-1;

c=x1;

}

b=0;

}

else if(abs(yd=y2-y1)<eps)

{

a=0;

if(x2>x1)

{

b=1;

c=-y1;

}

else

{

b=-1;

c=y1;

}

else

{

a=1;

b=(x2-x1)/(y1-y2);

c=-x1-b*y1;

if(yd>0)

{

a=-a; b=-b; c=-c;

}

l[ll].a=a; l[ll].b=b; l[ll].c=c; ll++;

}

inline void adde(int i,int j)

{

double a1=l[i].a,b1=l[i].b,c1=l[i].c;

double a2=l[j].a,b2=l[j].b,c2=l[j].c;

if(abs(a1)<eps&&abs(a2)<eps||abs(b1)<eps&&abs(b2)<eps)

return;

if(abs(a1/b1-a2/b2)<eps)

return;

double x,y;

if(abs(a1)<eps)

{

y=-c1/b1;

x=-(b2*y+c2)/a2;

}

else if(abs(b1)<eps)

{

x=-c1/a1;

y=-(c2+a2*x)/b2;

}

else

{

y=(a2/a1*c1-c2)/(b2-a2/a1*b1);

x=-(b1*y+c1)/a1;

}

L.push_back(E(x,y));

}

void init()

{

int i,j,k;

L.clear();

hd=-1;

el=ll=0;

for(i=0;i<n;i++)

scanf("%lf%lf",&x[i],&y[i]);

for(i=0;i<n-1;i++)

addl(x[i],y[i],x[i+1],y[i+1]);

addl(x[n-1],y[n-1],x[0],y[0]);

for(i=0;i<n-1;i++)

for(j=i+1;j<n;j++)

adde(i,j);

}

void solve()

{

int i,j,k;

double a,b,c,x,y;

list<E>::iterator lit;

for(i=0;i<ll;i++)

{

a=l[i].a; b=l[i].b; c=l[i].c;

for(lit=L.begin();lit!=L.end();)

{

x=lit->x; y=lit->y;

if(a*x+b*y+c<-eps)

L.erase(lit++);

else

lit++;

}

if(L.size())

puts("1");

else

puts("0");

}

int main()

{

while(~scanf("%d",&n)&&n)

{

init();

solve();

}

return 0;

}

最近都在练习计算几何的题目。感觉这类题有个特点是比较偏数学公式的推导，对复杂度的要求不会太高。

借这个机会好好复习下各种几何工具吧。

[POJ 3004]

发表回复

Subway planning

计算几何。

题意是，在二维平面上有n个点（不为原点且不重复），和距离值d，问最少从原点引出多少点射线，可以使得n个点离某条射线的最远距离都不超过d。

这题读完之后……基本是没有任何思路的。稍微分析一下可以发现，射线肯定都是刚好离某个点距离为d的。因此写了一个搜索，对任意一点，若未被覆盖，则（1）顺时侧置射线、（2）逆时侧置射线、（3）不置射线。结果TLE。又想了一些剪枝后，还是妥妥的TLE……

然后发现discuss基本是空的……就又google了一下题解，也去下载了题目的原始数据，花了整整一天时间，总算弄明白了。大致思路如下：

首先转换到极坐标系，并将每个点对应能被覆盖的射线位置范围视作区间，那么就可以将问题转化成区间覆盖问题：由于每个区间都是必定要被覆盖的，可以将区间按起始位置排序后，贪心地选择能按顺序地覆盖最多区间的位置放置射线，这可以通过取当前按序覆盖的区间中最左的右边界值来得到。每次下一个顺序区间无法被覆盖（左边界超过当前射线位置）时，贪心地重置射线位置为该区间的右边界值。所有n个区间处理完后便是最小覆盖射线数。

但这里有一个问题就是，极坐标是一个环形结构，无法确定哪个区间最为最左区间。考虑到这里n<=500，即使枚举每个区间为起始区间，算上排序，复杂度也只是O(n^2lgn)，是完全可以接受的。当然这里极坐标的计算形式以及弧度的处理还是有一些技巧的，比如atan2(y,x)函数直接根据y和x值返回取值范围在(-PI,PI]范围的弧度值，另外标程还用到了一个fmod(a,b)函数，是对浮点数算a - b*k = c，abs(c)

#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

#define PI 3.1415926535897932384626
#define eps 1e-8

int n,ans;
double d;

struct E
{
    double b,e;
    bool operator < (const E &p) const
    {
        return b<p.b;
    }
}e[1000],ee[1000];

void init()
{
    int i,j;
    double x,y,a,r,am;
    ans=0x7fffffff;
    for(i=j=0;i<n;i++)
    {
        scanf("%lf%lf",&x,&y);
        a=atan2(y,x);
        r=sqrt(y*y+x*x);
        if(r<d+eps)
            continue;
        am=asin(d/r);
        e[j].b=a-am;
        e[j].e=a+am;
        j++;
    }
    n=j;
    sort(e,e+n);
}

int calc(int i)
{
    int j,k,l;
    double top;
    for(j=i;j<n;j++)
    {
        ee[j-i].b=e[j].b;
        ee[j-i].e=e[j].e;
    }
    for(j=0;j<i;j++)
    {
        ee[n-i+j].b=e[j].b+2*PI;
        ee[n-i+j].e=e[j].e+2*PI;
    }
    for(i=l=1,top=ee[0].e;i<n;i++)
    {
        if(top<ee[i].b-eps)
        {
            l++;
            top=ee[i].e;
        }
        else if(top>ee[i].e+eps)
            top=ee[i].e;
    }
    return l;
}

void solve()
{
    int i;
    for(i=0;i<n;i++)
        ans=min(ans,calc(i));
    if(ans==0x7fffffff)
        ans=0;
    printf("%d\n",ans);
}

int main()
{
    scanf("%*d");
    while(~scanf("%d%lf",&n,&d))
    {
        init();
        solve();
    }
    return 0;
}

#include<cmath>

#include<cstdio>

#include<cstring>

#include<algorithm>

using namespace std;

#define PI 3.1415926535897932384626

#define eps 1e-8

int n,ans;

double d;

struct E

{

double b,e;

bool operator < (const E &p) const

{

return b<p.b;

}

}e[1000],ee[1000];

void init()

{

int i,j;

double x,y,a,r,am;

ans=0x7fffffff;

for(i=j=0;i<n;i++)

{

scanf("%lf%lf",&x,&y);

a=atan2(y,x);

r=sqrt(y*y+x*x);

if(r<d+eps)

continue;

am=asin(d/r);

e[j].b=a-am;

e[j].e=a+am;

j++;

}

n=j;

sort(e,e+n);

}

int calc(int i)

{

int j,k,l;

double top;

for(j=i;j<n;j++)

{

ee[j-i].b=e[j].b;

ee[j-i].e=e[j].e;

}

for(j=0;j<i;j++)

{

ee[n-i+j].b=e[j].b+2*PI;

ee[n-i+j].e=e[j].e+2*PI;

}

for(i=l=1,top=ee[0].e;i<n;i++)

{

if(top<ee[i].b-eps)

{

l++;

top=ee[i].e;

}

else if(top>ee[i].e+eps)

top=ee[i].e;

}

return l;

}

void solve()

{

int i;

for(i=0;i<n;i++)

ans=min(ans,calc(i));

if(ans==0x7fffffff)

ans=0;

printf("%d\n",ans);

}

int main()

{

scanf("%*d");

while(~scanf("%d%lf",&n,&d))

{

init();

solve();

}

return 0;

}

ps: 今天老师说可以公费买一些书（归实验室但实际是给我们看），京东也很合时宜地给了我几张优惠劵……结果便一发不可收拾了……稍微列下书单：语言类： Ruby元编程
 Python核心编程
 Python Cookbook
K&R
Erlang/OTP并发编程实战
 Node.js开发指南
 JavaScript语言精髓与编程实践

算法类：
TAOCP卷1
TAOCP卷2
TAOCP卷3
CLRS

IT文化类：
谁说大象不能跳舞？
代码的未来
 浪潮之巅
 图灵的秘密：他的生平、思想及论文解读

其他：
HTTP权威指南

其中有些是看过但出了新版的，比如CLRS、浪潮之巅；有些是可以有计划地读完的，如IT文化类的其他几本；有些是参考书，如语言类和其他；有些是纯粹是买来拜的……我不说你也知道是哪些……

[POJ 1988]

发表回复

Cube Stacking

并查集。

题意是，原有30,000个栈，每个栈中有一个cube，总共最多100,000个操作，每个操作可以是将一个栈叠到另一个上，或者是求某个cube下方有多少个cube。

很明显的”由cube指定的stack号来作叠置操作”暗示了要用并查集的。但以前写过的并查集仅能够实现（1）路径压缩；（2）按秩合并。也即f[i]表示的值可以是（1）栈编号(当f[i]>=0；（2）栈大小(当f[i]<0)。由此，不难推出，如果额外增设一个p[i]，记录每个cube到栈顶间有多少个cube，那么就可以有：栈大小 – 上方cube数 – 1 = 下方cube数。进一步分析p[i]的更新方式，每次作union(a,b)时，是将a整个放在b上的，也即此时p[b]=f[a]。但如果要使p[i]值正确，压缩路径前要记录原父cube，递归处理压缩路径后，将父cube的p值累加到本cube的p值上。跑出来只有500+ms，改成非递归可能才会快点。

#include<cstdio>
#include<cstring>

char s[2];
int m,f[30000],p[30000];

int fi(int i)
{
    if(f[i]<0) return i;
    int j=f[i];
    f[i]=fi(f[i]);
    p[i]+=p[j];
    return f[i];
}

void un(int a,int b)
{
    int fa=fi(a),fb=fi(b);
    p[fb]=f[fa];
    f[fa]+=f[fb];
    f[fb]=fa;
}

void init()
{
    memset(f,-1,sizeof f);
    memset(p,0,sizeof p);
}

void solve()
{
    int i,j,k,l;
    while(m--)
    {
        scanf("%s",s);
        if(s[0]=='M')
        {
            scanf("%d%d",&i,&j);
            un(i-1,j-1);
        }
        else
        {
            scanf("%d",&i);
            i--;
            j=fi(i);
            printf("%d\n",p[i]-f[j]-1);
        }
    }
}

int main()
{
    while(~scanf("%d",&m))
    {
        init();
        solve();
    }
    return 0;
}

#include<cstdio>

#include<cstring>

char s[2];

int m,f[30000],p[30000];

int fi(int i)

{

if(f[i]<0) return i;

int j=f[i];

f[i]=fi(f[i]);

p[i]+=p[j];

return f[i];

}

void un(int a,int b)

{

int fa=fi(a),fb=fi(b);

p[fb]=f[fa];

f[fa]+=f[fb];

f[fb]=fa;

}

void init()

{

memset(f,-1,sizeof f);

memset(p,0,sizeof p);

}

void solve()

{

int i,j,k,l;

while(m--)

{

scanf("%s",s);

if(s[0]=='M')

{

scanf("%d%d",&i,&j);

un(i-1,j-1);

}

else

{

scanf("%d",&i);

i--;

j=fi(i);

printf("%d\n",p[i]-f[j]-1);

}

int main()

{

while(~scanf("%d",&m))

{

init();

solve();

}

return 0;

}

[POJ 1177]

发表回复

Picture

题意大概是，给出N个矩形的描述，矩形间可能有重叠，问最后图形的总周长。

这题和早上做的November Rain都被人分类成线段树，但我愣是没有想明白，这个线段树可以怎么用。也都是数组处理了一下就A了。

说说这题，首先周长可以划分为平行于x轴和平行与y轴两部分。这两部分是独立的，可以分类处理，且处理方式类似。下面以与x轴平行为例说明。

首先将所有点坐标离散化，然后用一个struct数组，记录每条边的：y坐标、起止x离散坐标、下边界标记b（是某矩形下边界则为1，否则为0）。然后将2N条边先按y从小到大，再按x从小到大排序。初始化一个全0的数组t，大小为离散化x坐标的个数，表示某段边被覆盖的次数。然后遍历struct数组，对每条边，更新其包含的各线段j的覆盖情况，若边的b==1，则t[j]++，若此时t[j]==1则表示为图形的下边界，为周长的一部分；若边的b==0，则t[j]–，若此时t[j]==0则表示为图形的上边界，也为周长的一部分。

与Y轴平行的边，处理方式类似。由此便能在O(2N*lg(2N)+2NK)的时间内计算完整个图形的周长了，这里K是每条边包含离散线段的数目。貌似K最多是O(N)的，但题目没有这么刁钻的数据，最后也就跑了16MS。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

int n,r[5000][4],ei[20001],er[10000],d[10000],erl,pl,sum;
int t[20001],tl;

struct P
{
    int f,es,ed;
    char b;
    bool operator < (const P &p) const
    {
        if(f<p.f) return 1;
        if(f>p.f) return 0;
        return es<p.es;
    }
}p[10000];

void init()
{
    int i;
    for(i=0;i<n;i++)
    {
        scanf("%d%d%d%d",&r[i][0],&r[i][1],&r[i][2],&r[i][3]);
        r[i][0]+=10000; r[i][1]+=10000;
        r[i][2]+=10000; r[i][3]+=10000;
    }
    sum=0;
}

void solve()
{
    int i,j,k,l;
    for(i=tl=0;i<n;i++)
    {
        t[tl++]=r[i][0]; t[tl++]=r[i][2];
    }
    sort(t,t+tl);
    ei[t[0]]=0;
    er[0]=t[0];
    for(i=erl=1;i<tl;i++)
    {
        if(t[i]==t[i-1])
            continue;
        ei[t[i]]=erl;
        er[erl]=t[i];
        d[erl]=er[erl]-er[erl-1];
        erl++;
    }
    for(i=pl=0;i<n;i++)
    {
        p[pl].f=r[i][1]; p[pl].es=ei[r[i][0]];
        p[pl].ed=ei[r[i][2]]; p[pl].b=1; pl++;
        p[pl].f=r[i][3]; p[pl].es=ei[r[i][0]];
        p[pl].ed=ei[r[i][2]]; p[pl].b=0; pl++;
    }
    sort(p,p+pl);
    memset(t,0,sizeof t);
    for(i=0;i<pl;i++)
    {
        if(p[i].b)
        {
            for(j=p[i].es+1;j<=p[i].ed;j++)
            {
                t[j]++;
                if(t[j]==1)
                    sum+=d[j];
            }
        }
        else
        {
            for(j=p[i].es+1;j<=p[i].ed;j++)
            {
                t[j]--;
                if(t[j]==0)
                    sum+=d[j];
            }
        }
    }
    for(i=tl=0;i<n;i++)
    {
        t[tl++]=r[i][1]; t[tl++]=r[i][3];
    }
    sort(t,t+tl);
    ei[t[0]]=0;
    er[0]=t[0];
    for(i=erl=1;i<tl;i++)
    {
        if(t[i]==t[i-1])
            continue;
        ei[t[i]]=erl;
        er[erl]=t[i];
        d[erl]=er[erl]-er[erl-1];
        erl++;
    }
    for(i=pl=0;i<n;i++)
    {
        p[pl].f=r[i][0]; p[pl].es=ei[r[i][1]];
        p[pl].ed=ei[r[i][3]]; p[pl].b=1; pl++;
        p[pl].f=r[i][2]; p[pl].es=ei[r[i][1]];
        p[pl].ed=ei[r[i][3]]; p[pl].b=0; pl++;
    }
    sort(p,p+pl);
    memset(t,0,sizeof t);
    for(i=0;i<pl;i++)
    {
        if(p[i].b)
        {
            for(j=p[i].es+1;j<=p[i].ed;j++)
            {
                t[j]++;
                if(t[j]==1)
                    sum+=d[j];
            }
        }
        else
        {
            for(j=p[i].es+1;j<=p[i].ed;j++)
            {
                t[j]--;
                if(t[j]==0)
                    sum+=d[j];
            }
        }
    }
    printf("%d\n",sum);
}

int main()
{
    while(~scanf("%d",&n))
    {
        init();
        solve();
    }
    return 0;
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

#include<cstdio>

#include<cstring>

#include<algorithm>

using namespace std;

int n,r[5000][4],ei[20001],er[10000],d[10000],erl,pl,sum;

int t[20001],tl;

struct P

{

int f,es,ed;

char b;

bool operator < (const P &p) const

{

if(f<p.f) return 1;

if(f>p.f) return 0;

return es<p.es;

}

}p[10000];

void init()

{

int i;

for(i=0;i<n;i++)

{

scanf("%d%d%d%d",&r[i][0],&r[i][1],&r[i][2],&r[i][3]);

r[i][0]+=10000; r[i][1]+=10000;

r[i][2]+=10000; r[i][3]+=10000;

}

sum=0;

}

void solve()

{

int i,j,k,l;

for(i=tl=0;i<n;i++)

{

t[tl++]=r[i][0]; t[tl++]=r[i][2];

}

sort(t,t+tl);

ei[t[0]]=0;

er[0]=t[0];

for(i=erl=1;i<tl;i++)

{

if(t[i]==t[i-1])

continue;

ei[t[i]]=erl;

er[erl]=t[i];

d[erl]=er[erl]-er[erl-1];

erl++;

}

for(i=pl=0;i<n;i++)

{

p[pl].f=r[i][1]; p[pl].es=ei[r[i][0]];

p[pl].ed=ei[r[i][2]]; p[pl].b=1; pl++;

p[pl].f=r[i][3]; p[pl].es=ei[r[i][0]];

p[pl].ed=ei[r[i][2]]; p[pl].b=0; pl++;

}

sort(p,p+pl);

memset(t,0,sizeof t);

for(i=0;i<pl;i++)

{

if(p[i].b)

{

for(j=p[i].es+1;j<=p[i].ed;j++)

{

t[j]++;

if(t[j]==1)

sum+=d[j];

}

else

{

for(j=p[i].es+1;j<=p[i].ed;j++)

{

t[j]--;

if(t[j]==0)

sum+=d[j];

}

for(i=tl=0;i<n;i++)

{

t[tl++]=r[i][1]; t[tl++]=r[i][3];

}

sort(t,t+tl);

ei[t[0]]=0;

er[0]=t[0];

for(i=erl=1;i<tl;i++)

{

if(t[i]==t[i-1])

continue;

ei[t[i]]=erl;

er[erl]=t[i];

d[erl]=er[erl]-er[erl-1];

erl++;

}

for(i=pl=0;i<n;i++)

{

p[pl].f=r[i][0]; p[pl].es=ei[r[i][1]];

p[pl].ed=ei[r[i][3]]; p[pl].b=1; pl++;

p[pl].f=r[i][2]; p[pl].es=ei[r[i][1]];

p[pl].ed=ei[r[i][3]]; p[pl].b=0; pl++;

}

sort(p,p+pl);

memset(t,0,sizeof t);

for(i=0;i<pl;i++)

{

if(p[i].b)

{

for(j=p[i].es+1;j<=p[i].ed;j++)

{

t[j]++;

if(t[j]==1)

sum+=d[j];

}

else

{

for(j=p[i].es+1;j<=p[i].ed;j++)

{

t[j]--;

if(t[j]==0)

sum+=d[j];

}

printf("%d\n",sum);

}

int main()

{

while(~scanf("%d",&n))

{

init();

solve();

}

return 0;

}

[POJ 2888]

发表回复

Magic Bracelet

数论。

本来这题是在分类表里靠后的位置的，但由于最近在啃具体数学，第四章讲了“莫比乌斯反演”，就顺势把题做一下。

题意是这样的，有一个长度为n的珠串，每个珠子的颜色有m种，但其中有k对颜色是不能相邻的，问在剔除因旋转导致的重复后总共有多少种可能的珠串。

先讲这题的简化版，是POJ 2154，区别在于没有珠子间不能连接的限制。

其基本的思想仍然是Polya定理。但是这里由于n值太大，无法直接枚举出所有的置换群。于是需要考虑将具有相同数量循环节的置换群合并处理。具体的合并方式是要利用到欧拉函数phi()的性质的。总共的置换群有n个，对n的每个因子d，有n/d个循环节的置换群其每个循环节长度为d，而这样的循环群总数是phi(d)个。又因为欧拉函数满足sum_{d\n} phi(d) == n，因此计数式子就可以转化为 (sum_{d\n} phi(d) * n^(n/d)) / n。计算phi(d)的时间复杂度是O(lgd)，而n的因子总数是不超过1000的（最多9个不同因子），n的n/d次方是可以在O(lg(n/d))时间内计算得到的，由此问题便能在合理时间内求解了。

另外就是计算的时候，要注意利用模运算的性质，使用int来处理（比long long快很多），同时尽量减少进行模运算的次数，否则还是会TLE的。

下面是2154的代码：

#include<cstdio>
#include<cstring>
#include<cmath>

#define pl 4000

int n,m,o;
int p[pl]={2,3},pn[pl][2],pnl;

void initp()
{
    int i,j,k,l;
    for(i=2;i<pl;i++)
    {
        for(j=p[i-1]+2;1;j+=2)
        {
            for(k=0,l=sqrt(j);p[k]<=l&&j%p[k];k++);
            if(p[k]>l)
            {
                p[i]=j;
                break;
            }
        }
    }
}

inline int phi(int d)
{
    int i,j,k;
    for(i=0,j=d,k=sqrt(d);p[i]<=k;i++)
        if(d%p[i]==0)
        {
            j-=j/p[i];
            while(d%p[i]==0)
                d/=p[i];
        }
    if(d>1)
        j-=j/d;
    return j%m;
}

inline int pm(int d)
{
    int i,j,k;
    k=n%m;
    for(i=1;i<=d;i<<=1);
    i>>=1;
    for(j=1;i;i>>=1)
    {
        j=j*j%m;
        if(i&d)
            j=j*k%m;
    }
    return j;
}

void init()
{
    int i,j,k,l;
    memset(pn,0,sizeof pn);
    for(i=pnl=0,j=n,k=sqrt(n);p[i]<=k&&j>1;i++)
    {
        if(j%p[i]==0)
        {
            pn[pnl][0]=p[i];
            while(j%p[i]==0)
            {
                j/=p[i];
                pn[pnl][1]++;
            }
            pnl++;
        }
    }
    if(j>1)
    {
        pn[pnl][0]=j;
        pn[pnl][1]=1;
        pnl++;
    }
}

void calc(int i,int d)
{
    if(i==pnl)
    {
        o=(o+phi(d)*pm(n/d-1))%m;
        return;
    }
    int j,k,l;
    for(j=0,k=1;j<=pn[i][1];j++,k*=pn[i][0])
        calc(i+1,d*k);
}

void solve()
{
    o=0;
    calc(0,1);
    printf("%d\n",o);
}

int main()
{
    initp();
    scanf("%*d");
    while(~scanf("%d%d",&n,&m))
    {
        init();
        solve();
    }
    return 0;
}

100

101

102

103

104

105

106

107

108

109

110

111

#include<cstdio>

#include<cstring>

#include<cmath>

#define pl 4000

int n,m,o;

int p[pl]={2,3},pn[pl][2],pnl;

void initp()

{

int i,j,k,l;

for(i=2;i<pl;i++)

{

for(j=p[i-1]+2;1;j+=2)

{

for(k=0,l=sqrt(j);p[k]<=l&&j%p[k];k++);

if(p[k]>l)

{

p[i]=j;

break;

}

inline int phi(int d)

{

int i,j,k;

for(i=0,j=d,k=sqrt(d);p[i]<=k;i++)

if(d%p[i]==0)

{

j-=j/p[i];

while(d%p[i]==0)

d/=p[i];

}

if(d>1)

j-=j/d;

return j%m;

}

inline int pm(int d)

{

int i,j,k;

k=n%m;

for(i=1;i<=d;i<<=1);

i>>=1;

for(j=1;i;i>>=1)

{

j=j*j%m;

if(i&d)

j=j*k%m;

}

return j;

}

void init()

{

int i,j,k,l;

memset(pn,0,sizeof pn);

for(i=pnl=0,j=n,k=sqrt(n);p[i]<=k&&j>1;i++)

{

if(j%p[i]==0)

{

pn[pnl][0]=p[i];

while(j%p[i]==0)

{

j/=p[i];

pn[pnl][1]++;

}

pnl++;

}

if(j>1)

{

pn[pnl][0]=j;

pn[pnl][1]=1;

pnl++;

}

void calc(int i,int d)

{

if(i==pnl)

{

o=(o+phi(d)*pm(n/d-1))%m;

return;

}

int j,k,l;

for(j=0,k=1;j<=pn[i][1];j++,k*=pn[i][0])

calc(i+1,d*k);

}

void solve()

{

o=0;

calc(0,1);

printf("%d\n",o);

}

int main()

{

initp();

scanf("%*d");

while(~scanf("%d%d",&n,&m))

{

init();

solve();

}

return 0;

}

回到2888。这题额外增加了珠子间的连接限制，对应的处理方式是这样的：初始化矩阵a[m][m]元素全为1，若i和j不能相邻，则a[i][j]=a[j][i]=0，然后计算b = a^d，则长度为d的珠串其总可能数是sum{b[i][i]}。这里当i<=j时，(a^d)[i][j]表示的是，以种类i开始长度为d，结尾能够与种类j的珠子相连的珠串总数。至于为什么是这样，推一下就明白了。于是这里计数式子就变成了(sum_{d\n} phi(d) * sum{(a^(n/d))[i][i]}) / n。落实到具体实现时，在对n做除法时，要转化成乘以模运算下n的乘法逆元。前面的每一步处理也要控制好在int的范围内以及限制模运算的使用次数。

#include<cstdio>
#include<cstring>
#include<cmath>

#define pl 4000
#define mod 9973

int n,m,o;
int p[pl]={2,3},pn[pl][2],pnl;
int a[10][10],b[10][10],t[10][10];

void initp()
{
    int i,j,k,l;
    for(i=2;i<pl;i++)
    {
        for(j=p[i-1]+2;1;j+=2)
        {
            for(k=0,l=sqrt(j);p[k]<=l&&j%p[k];k++);
            if(p[k]>l)
            {
                p[i]=j;
                break;
            }
        }
    }
}

int phi(int d)
{
    int i,j,k;
    for(i=0,j=d,k=sqrt(d);p[i]<=k;i++)
        if(d%p[i]==0)
        {
            j-=j/p[i];
            while(d%p[i]==0)
                d/=p[i];
        }
    if(d>1)
        j-=j/d;
    return j%mod;
}

void mul(int a[10][10],int b[10][10])
{
    int i,j,k,l;
    memset(t,0,sizeof t);
    for(i=0;i<m;i++)
        for(j=0;j<m;j++)
        {
            for(k=0;k<m;k++)
                t[i][j]+=a[i][k]*b[k][j];
            t[i][j]%=mod;
        }
    memcpy(a,t,sizeof t);
}

int pm(int d)
{
    int i,j,k,l;
    memset(b,0,sizeof b);
    for(i=0;i<m;i++)
        b[i][i]=1;
    for(i=1;i<=d;i<<=1);
    for(i>>=1;i;i>>=1)
    {
        mul(b,b);
        if(i&d)
            mul(b,a);
    }
    for(i=j=0;i<m;i++)
        j+=b[i][i];
    return j%mod;
}

void init()
{
    int i,j,k,l;
    for(i=0;i<m;i++)
        for(j=0;j<m;j++)
            a[i][j]=1;
    while(o--)
    {
        scanf("%d%d",&i,&j);
        a[i-1][j-1]=a[j-1][i-1]=0;
    }
    memset(pn,0,sizeof pn);
    for(i=pnl=0,j=n,k=sqrt(n);p[i]<=k&&j>1;i++)
    {
        if(j%p[i]==0)
        {
            pn[pnl][0]=p[i];
            while(j%p[i]==0)
            {
                j/=p[i];
                pn[pnl][1]++;
            }
            pnl++;
        }
    }
    if(j>1)
    {
        pn[pnl][0]=j;
        pn[pnl][1]=1;
        pnl++;
    }
}

void calc(int i,int d)
{
    if(i==pnl)
    {
        o=(o+phi(d)*pm(n/d))%mod;
        return;
    }
    int j,k,l;
    for(j=0,k=1;j<=pn[i][1];j++,k*=pn[i][0])
        calc(i+1,d*k);
}

void solve()
{
    o=0;
    calc(0,1);
    int i,j;
    for(i=1,j=n%mod;(i*j)%mod!=1;i++);
    printf("%d\n",o*i%mod);
}

int main()
{
    initp();
    scanf("%*d");
    while(~scanf("%d%d%d",&n,&m,&o))
    {
        init();
        solve();
    }
    return 0;
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

#include<cstdio>

#include<cstring>

#include<cmath>

#define pl 4000

#define mod 9973

int n,m,o;

int p[pl]={2,3},pn[pl][2],pnl;

int a[10][10],b[10][10],t[10][10];

void initp()

{

int i,j,k,l;

for(i=2;i<pl;i++)

{

for(j=p[i-1]+2;1;j+=2)

{

for(k=0,l=sqrt(j);p[k]<=l&&j%p[k];k++);

if(p[k]>l)

{

p[i]=j;

break;

}

int phi(int d)

{

int i,j,k;

for(i=0,j=d,k=sqrt(d);p[i]<=k;i++)

if(d%p[i]==0)

{

j-=j/p[i];

while(d%p[i]==0)

d/=p[i];

}

if(d>1)

j-=j/d;

return j%mod;

}

void mul(int a[10][10],int b[10][10])

{

int i,j,k,l;

memset(t,0,sizeof t);

for(i=0;i<m;i++)

for(j=0;j<m;j++)

{

for(k=0;k<m;k++)

t[i][j]+=a[i][k]*b[k][j];

t[i][j]%=mod;

}

memcpy(a,t,sizeof t);

}

int pm(int d)

{

int i,j,k,l;

memset(b,0,sizeof b);

for(i=0;i<m;i++)

b[i][i]=1;

for(i=1;i<=d;i<<=1);

for(i>>=1;i;i>>=1)

{

mul(b,b);

if(i&d)

mul(b,a);

}

for(i=j=0;i<m;i++)

j+=b[i][i];

return j%mod;

}

void init()

{

int i,j,k,l;

for(i=0;i<m;i++)

for(j=0;j<m;j++)

a[i][j]=1;

while(o--)

{

scanf("%d%d",&i,&j);

a[i-1][j-1]=a[j-1][i-1]=0;

}

memset(pn,0,sizeof pn);

for(i=pnl=0,j=n,k=sqrt(n);p[i]<=k&&j>1;i++)

{

if(j%p[i]==0)

{

pn[pnl][0]=p[i];

while(j%p[i]==0)

{

j/=p[i];

pn[pnl][1]++;

}

pnl++;

}

if(j>1)

{

pn[pnl][0]=j;

pn[pnl][1]=1;

pnl++;

}

void calc(int i,int d)

{

if(i==pnl)

{

o=(o+phi(d)*pm(n/d))%mod;

return;

}

int j,k,l;

for(j=0,k=1;j<=pn[i][1];j++,k*=pn[i][0])

calc(i+1,d*k);

}

void solve()

{

o=0;

calc(0,1);

int i,j;

for(i=1,j=n%mod;(i*j)%mod!=1;i++);

printf("%d\n",o*i%mod);

}

int main()

{

initp();

scanf("%*d");

while(~scanf("%d%d%d",&n,&m,&o))

{

init();

solve();

}

return 0;

}

虽然上面写了这么多但很多都是现学现卖的OTL。不过数论还真是很有意思的东西……

[POJ 3286]

发表回复

How many 0’s?

数学。

比较不擅长的题目类型，虽然一直以来都挺喜欢数学的；）

问的是输入unsigned int m和n，问[m, n]的所有数字打印出来后，总共包含多少个0。

题意非常明确的，其实就是要推出函数calc(d)，能返回0到d所有0的个数，那么calc(n)-calc(m-1)就是结果。

对于某个具体的d，这里基本的思路是将其包含的数按范围划分，例如d=109250时，首先拆成[0, 100000]，[100001, 109000]，[109001, 109200]和[109201, 109250]。那么就可以分情况讨论各个范围内数字所含0的总数，最后累加起来即可。

这里采用的方式是从高位开始拆数。例如，将[0, 109250]包括的0拆成三部分：（1）[0, 100000]，（2）[0, 9250]，（3）以”10″为前缀导致[0, 9250]额外引入的0。那么就可以对[0, 9250]迭代地计算其中包含的0了。也即，此时算法复杂度是和d的位数线性相关的，基本上是O(1)。下面分别讨论三部分含0数目的计算方法。

（1）这里可以预处理，例如a[i]=10^i时，分别计算[1, a[i]]以及[a[i]+1, a[i]*2]范围内所含0的总数，设为b[i]和c[i]。例如a[2]=10^2=100时，b[i]为[1, 100]内0的总数，c[i]为[101, 200]内0的总数。这样处理的原因是，（1）中每次都是拆最高位的，这样当最高位为k时，即为b[i]+(k-1)*c[i]。这里b[i]和c[i]有递推关系，当然其实暴力打表也可以的。

（2）这部分是迭代的，和原本的d处理方法相同；

（3）这部分比较麻烦。首先要记录前缀中含0的个数，然后由d去除最高位后剩余的dd计算需要增加多少个0。这里分情况讨论一下即可。如果前缀有j个0，那么最前面的0包括dd*j个，然后再额外处理后面每一位的情况。

看了别人的基本思路，自己推起来也还是磕磕绊绊。表达起来就更是觉得繁琐了……

#include<cstdio>
#define ll long long

ll a[11],b[11],c[11];
ll m,n;

void init()
{
    ll i,j,k,l;
    a[0]=1;
    for(i=1,k=l=0;i<11;i++,l=l*10+9,k+=l)
    {
        a[i]=a[i-1]*10;
        b[i]=b[i-1]+c[i-1]*9+1;
        c[i]=b[i]+k;
    }
}

ll calc(ll d)
{
    if(!d) return 0;
    ll i,j,k,dd,sum=0;
    for(i=0;i<11&&a[i]<=d;i++);
    i--;
    dd=d-a[i];
    sum=b[i];
    while(dd>=a[i])
    {
        dd-=a[i];
        sum+=c[i];
    }
    if(dd)
    {
        for(i--,j=0;i>0&&a[i]>dd;i--,j++);
        sum+=dd*j;
        while(i)
        {
            sum+=a[i]-1;
            i--;
        }
    }
    return sum+calc(dd);
}

void solve()
{
    if(m==0) 
        printf("%lld\n",calc(n)+1);
    else
        printf("%lld\n",calc(n)-calc(m-1));
}

int main()
{
    init();
    while(~scanf("%lld%lld",&m,&n)&&m!=-1)
        solve();
    return 0;
}

#include<cstdio>

#define ll long long

ll a[11],b[11],c[11];

ll m,n;

void init()

{

ll i,j,k,l;

a[0]=1;

for(i=1,k=l=0;i<11;i++,l=l*10+9,k+=l)

{

a[i]=a[i-1]*10;

b[i]=b[i-1]+c[i-1]*9+1;

c[i]=b[i]+k;

}

ll calc(ll d)

{

if(!d) return 0;

ll i,j,k,dd,sum=0;

for(i=0;i<11&&a[i]<=d;i++);

i--;

dd=d-a[i];

sum=b[i];

while(dd>=a[i])

{

dd-=a[i];

sum+=c[i];

}

if(dd)

{

for(i--,j=0;i>0&&a[i]>dd;i--,j++);

sum+=dd*j;

while(i)

{

sum+=a[i]-1;

i--;

}

return sum+calc(dd);

}

void solve()

{

if(m==0)

printf("%lld\n",calc(n)+1);

else

printf("%lld\n",calc(n)-calc(m-1));

}

int main()

{

init();

while(~scanf("%lld%lld",&m,&n)&&m!=-1)

solve();

return 0;

}

[POJ 3301]

发表回复

Texas Trip

三分法。

其实一开始我是二分做的，二分的对象是正方形的边长，判断可行行则是将整幅图每次旋转一个微小角度，计算与坐标轴平行覆盖所有点的最小正方形。虽然这题精度和数据规模都一般，但还是妥妥的TLE了。于是看了讨论，又参考了这篇文章。

思路还是很清晰的，旋转范围是[0,pi/2]，在这范围内最短边长值是凹函数。于是对角度三分之后，计算所有点坐标中x、y两方向上的最大差值，并取较大值为此时正方形边长。迭代直到精度足够即可。

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;

int n;
double r[30],a[30];
const double eps=1e-8;
const double ma=3.141592653589793/2;

void init()
{
    int i;
    double x,y;
    for(i=0;i<n;i++)
    {
        scanf("%lf%lf",&x,&y);
        r[i]=sqrt(x*x+y*y);
        a[i]=asin(y/r[i]);
        if(x<0)
        {
            if(y>0)
                a[i]=ma*2-a[i];
            else
                a[i]=-ma*2-a[i];
        }
    }
}

double calc(double m)
{
    int i;
    double x,y,lx,rx,by,ty;
    lx=by=1e30;
    rx=ty=-1e30;
    for(i=0;i<n;i++)
    {
        x=r[i]*cos(a[i]+m);
        y=r[i]*sin(a[i]+m);
        lx=min(lx,x);
        rx=max(rx,x);
        by=min(by,y);
        ty=max(ty,y);
    }
    return max(rx-lx,ty-by);
}

void solve()
{
    double l,h,m,mm,e,ee;
    for(l=0,h=ma;l<h-eps;)
    {
        m=(l+h)/2;
        mm=(m+h)/2;
        e=calc(m);
        ee=calc(mm);
        if(e<ee)
            h=mm;
        else
            l=m;
    }
    e=calc(l);
    printf("%.2f\n",e*e);
}

int main()
{
    scanf("%*d");
    while(~scanf("%d",&n))
    {
        init();
        solve();
    }
    return 0;
}

#include<cstdio>

#include<cstring>

#include<cmath>

#include<algorithm>

using namespace std;

int n;

double r[30],a[30];

const double eps=1e-8;

const double ma=3.141592653589793/2;

void init()

{

int i;

double x,y;

for(i=0;i<n;i++)

{

scanf("%lf%lf",&x,&y);

r[i]=sqrt(x*x+y*y);

a[i]=asin(y/r[i]);

if(x<0)

{

if(y>0)

a[i]=ma*2-a[i];

else

a[i]=-ma*2-a[i];

}

double calc(double m)

{

int i;

double x,y,lx,rx,by,ty;

lx=by=1e30;

rx=ty=-1e30;

for(i=0;i<n;i++)

{

x=r[i]*cos(a[i]+m);

y=r[i]*sin(a[i]+m);

lx=min(lx,x);

rx=max(rx,x);

by=min(by,y);

ty=max(ty,y);

}

return max(rx-lx,ty-by);

}

void solve()

{

double l,h,m,mm,e,ee;

for(l=0,h=ma;l<h-eps;)

{

m=(l+h)/2;

mm=(m+h)/2;

e=calc(m);

ee=calc(mm);

if(e<ee)

h=mm;

else

l=m;

}

e=calc(l);

printf("%.2f\n",e*e);

}

int main()

{

scanf("%*d");

while(~scanf("%d",&n))

{

init();

solve();

}

return 0;

}

又学到了很实用的算法。 ^ ^